Sudoku
Sudoku (Bahasa Jepun: 数独, sūdoku), kadangkala dieja Su Doku, adalah permainan berdasarkan logik juga dikenali sebagai Number Place di Amerika Syarikat. Matlamat permainan kanonikal ini adalah untuk memasukkan suatu digit bernombor dari 1 ke 9 dalam satu sel grid 9X9 dengan subgrid 3X3 yang dipanggil 'kawasan' bermula dengan beberapa nombor 'diberi' dalam sesetengah sel lain. Setiap sel dan kawasan hanya boleh mempunyai satu kali sahaja suatu nombor digit dari 1 ke 9 sahaja. Menghabiskan permainan ini memerlukan kesabaran dan kemahiran berfikir secara logik. Walaupun ia mula diterbitkan pada tahun 1979, ia mula mendapat nama di Jepun pada tahun 1986 dan pada peringkat antarabangsa pada tahun 2005. Sebab mengapa popularitinya naik dengan begitu lambat masa yang diambil masih menjadi tanda tanya.
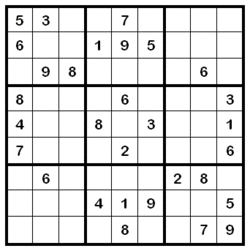
Pengenalan sunting
Peristilahan Sudoku memberi maksud "nombor bersendirian" dalam bahasa Jepun; dan merupakan hak cipta rasmi Nikoli Co. Ltd di Jepun. Penerbit Jepun yang lain biasanya merujuk permainan ini dengan gelaran Nanpure yang menjadi Number Place di dalam bahasa Inggeris Amerika. Nama ini dikatakan merupakan nama asal. Perkataan Sudoku disebut tampa apa-apa perubahan dengan pengalihan bahasa daripada Jepun ke Melayu.
Nombor-nombor yang diaplikasikan dalam Sudoku hanyalah bagi tujuan keselesaan semata-mata dan penggiraan matematik antara nombor-nombor tidak relevan sama sekali. Nombor-nombor ini boleh digantikan dengan bentuk-bentuk seperti bulatan, segi tiga dan segi empat sekalipun, asalkan ketara perbezaannya. Warna juga boleh digunakan. Majalah Sudoku Scramblets dimiliki Penny Press dan Sudoku Word milik Knight Features Syndicate menggunakan huruf abjad manakala Dell Magazines yang merupakan asal permainan ini menggunakan nombor bagi Number Place dalam majalahnya sejak tahun 1979. Dalam rencana ini, nombor digunakan.
Daya tarikan permainan ini adalah kesenangan peraturannya untuk menghabiskan, tetapi kesusahan daya logik yang diperlukan untuk melakukannya. Sudoku disyorkan oleh sesetengah guru untuk menaikan kebolehan seseorang dalam pemikiran dan penyelesaian masalah secara logik. Taraf kesusahannya boleh ditentukan untuk para pemainnya. Permainan ini seringkali didatangkan percuma dalam sumber-sumber media seperti surat khabar dan juga boleh dicipta oleh program aplikasi komputer yang khusus bagi tujuan ini.
Permainan ini telah mula muncul pada peringkat antarabangsa pada awal tahun 2005 dan menjadi popular di Amerika Syarikat, Australia, India, Britain dan Israel dan tiba di Malaysia beberapa bulan selepas itu dengan terbitnya ia pada akhbar harian bahasa Inggeris The Star. Malay Mail dan New Straits Times dalam pulloutnya '6' juga kini menerbitkan Sudoku pada setiap penghujung minggu.
Terminologi dan peraturan permainan sunting
Permainan seringkali berupa grid 9×9 grid, didalami 3×3 subgrid dipanggil "kawasan" (panggillan lain merupakan "kotak", "petak", dan sebagainya). Sesetengah sel disediakan dengan nombor yang telah diisikan, dipanggil "diberi" (kadangkala "petunjuk") Matlamatnya adalah untuk mengisikan setiap sel dan kawasan sehinggalah nombor 1 sehingga 9 diisi dalam suatu kawasan kesemuanya. Setiap nombor dalam penyelesaian dengan sendirinya hanya timbul sekali dalam tiga "arah". Disebabkan itulah nama asal permainan ini wujud - Nombor Bersendirian.
Cara penyelesaian sunting
Strategi menyelesaikan permainan ini boleh dikira mempunyai kombinasi tiga proses: Pencarian, Tulis Tanda dan Analisa.
Pencarian sunting
Pencarian dilakukan pada permulaan permainan dan kerap kalinya pada waktu penyelesaian. Carian mungkin terpaksa dilakukan diantara banyak kali ketika analisa. Pencarian terdiri daripada dua teknik mudah:
- Silang-hapus: pencarian secara mengufuk atau menjajar untuk mengenalpasti garisan sesuatu kawasan yang mempunyai sesuatu nombor untuk dihapuskan. Proses ini diteruskan dengan mengufuk (atau menjajar). Untuk penghabisan yang lebih cepat, nombor dicari dalam urutan kekerapannya. Adalah penting untuk melakukan ini dengan sistematik, dengan menandakan nombor-nombor yang patut 1–9.
- Mengira 1–9 dalam kawasan, mengufuk dan menjajar untuk mengenalpasti nombor yang tiada. Mengira berdasarkan nombor terakhir yang dijumpai menjanjikan penyelesaikan yang lebih cepat. Ia juga menjadi nyata (biasanya dalam permainan yang lebih sukar) yang nilai angka yang patut dalam satu sel boleh dikira dengan mengira ke belakang— iaitu, mencari di dalam satu kawasan, secara menjajar dan mengufuk untuk nilai angka yang tidak boleh dinampakkan apa yang tinggal.
Para pemain yang berpengalaman mencari "kontingensi" apabila mengira — iaitu, mencari sehingga satu lokasi nombor di dalam garisan mengufuk atau menjajar ataupun satu kawasan dengan dua atau tiga sel. Apabila kesemua sel itu berada pada garisan ufuk atau dataran yang sama dan kawasan, mereka boleh digunakan bagi tujuan hampusan semasa silang-hampus dan mengira. (Contoh di Puzzle Japan). Yang paling sukar sekali mungkin memakan ramai kontingensi untuk dikenalpasti, mungkin pada pelbagai arah ataupun arah yang bersilangan garisannya, dan sejurus memaksa para pemain menggunakan tulis tanda seperti yang diterangkan dibawah. Permainan yang boleh diselesaikan dengan pencarian semata-mata tampa memerlukan kontingensi digelar "senang". Permainan yang lebih sukar secara definasinya tidaklah termasuk yang memerlukan kontingensi untuk diselesaikan.
Tulis tanda sunting
Pencarian berhenti apabila tiada nombor-nombor lain boleh dijumpai. Dari ketika ini, adalah perlu sedikit analisis berdasarkan logik digunakan. Ramai mendapati bahawa adalah senang untuk menghalakan analisa ini dengan membuat tanda nombor-nombor yang berpotensi dalam sel-sel yang tidak bernombor. Terdapat dua cara menulis tanda: noktah dan subskrip.
- Noktah pula adalah paten titik dengan titik di sudut bahagian tangan kiri menandakan 1 dan titik di sudut bahagian tangan kanan menandakan 9. Cara ini boleh digunakan pada permainan yang asal. Ketelitian diperlukan apabila membuat noktah kerana noktah yang disalah letak atau kesan kotoran lain boleh menyebabkan kecelaruan dan mungkin tidak senang dipadamkan dengan tidak menambah minyak kedalam api! Menggunakan pensil dengan cara ini disyorkan.
- Noktah subskrip adalah apabila nombor-nombor yang difikirkan berpotensi ditulis dalam sel kosong. Keburukan cara ini adalah kebanyakan sel-sel cetakan surat khabar terlalu kecil untuk tujuan ini. Jika para pemain menggunakan cara ini, biasanya satu salinan yang digandakan saiznya dihasilkan atau menggunakan pensel yang halus seperti mekanik.
Cara teknik alternatif yang sesetengah mendapati lebih senang adalah menandakan sel yang "tidak mungkin" menjadi. Maka satu sel akan bermula kosong dan apabila lebihan "ketidak mungkinan" diketahui ia semakin diisi. Apabila hanya satu nilai angka tiada, itulah nilai angka yang sepatutnya.
Analisa sunting
Dua cara mendekati analisa adalah "penghampusan nombor" dan "bagaimana-jika".
- Dalam penghampusan nombor, kemajuan didasarkan penghampusan nombor-nombor yang difikirkan sesuai daripada satu atau lebih sel untuk meninggalkan satu pilihan. Selepas setiap jawapan dicapai, satu lagi pencarian boleh dilakukan —biasanya untuk melihat kesan nombor yang terakhir lalu. Terdapat beberapa taktik penghampusan, semuanya berdasarkan peraturan-perturan mudah diatas, yang mempunyai kepentingan dan kegunaan tertentu, termasuk:
- Pemberian satu set n sel dalam mana-mana satu blok, secara mendatar atau mengufuk hanya boleh menerima nombor lain n. Inilah asas bagi teknik "calon bagi penghampusan yang tidak tercapai" yang dibincangkan dibawah.
- Setiap nombor yang dipertimbangkan, 1–9, mestilah pada akhirnya menjadi satu bentuk tersendiri yang konsisten. Inilah asas bagi teknik analisa yang bertaraf tinggi yang memerlukan kepekaan terhadap kemungkinan bagi satu nombor yang diberikan. Hanya sesetengah kemungkinan seperti "closed circuit" atau "n×n grid" wujud (yang dipanggil dengan nama-nama aneh seperti X-Wing atau Swordfish disamping yang lain). Jika bentuk-bentuk ini boleh dikenalpasti, penghampusan kemungkinan-kemungkinan yang dikenalpasti berada pada jangkaan luar grid kadangkala boleh dicapai.
- Salah satu daripada taktik penghampusan adalah "penghampusan tidak terhingga". Sel-sel yang mempunyai set nombor yang sama dikatakan bertemu apabila kuantiti nombor-nombor cadangan adalah sama dengan jumlah sel-sel yang mempunyai mereka; secara terasnya, ini adalah kontingensi yang muncul secara semulajadi. Sebagai contoh, sel-sel dikatakan sama dalam satu garisan mengufuk, mendatar, atau kawasan (skop) jika dua sel ada pasangan dua nombor yang sama seperti p,q atau pasangan tiga nombor yang sama p,q,r dan tiada lagi yang lain. Letakan nombor dalam skop yang satu lagi akan menyebabkan penyelesaikan bagi sel-sel yang satu lagi tidak mungkin; maka, nombor cadangan (p,q,r) yang muncul dalam sel-sel yang tidak sama
Salah satu taktik penyingkiran biasa adalah "pemadaman calon tak sepadan - unmatched candidate deletion". Sel boleh dianggap sepadan sekiranya bilangan nombor bagi setiap sel adalah sama dengan bilangan sel-sel yang mengandunginya; ini adalah kontigensi tidak sengaja - coincident contigencies. Contohnya, sel-sel dianggap sepadan dalam satu barisan, lajur, atau kawasan sekiranya: - 2 sel mengandungi 2 nombor calon yang sepadan (p,q) bagi setiap satu sel dan tidak nombor lain, atau - 3 sel mengandungi 3 nombor calon yang sepadan (p,q,r) bagi setiap satu sel dan tidak nombor lain.
Taraf kesukaran sunting
Permainan yang disiarkan seringkali diberi taraf dari segi kesukarannya. Agak memeranjatkan, nilai yang diberikan hanya mempunyai sedikit atau tiada kaitan dengan kesukaran permainan tersebut. Permainan dengan jumlah penyelesaian minima diberikan mungkin mudah diselesaikan, dan permainan yang melebihi nombor purata penyelesaian mungkin amat sukar diselesaikan. Ianya berdasarkan kaitan nombor dan bukannya jumlah nombor yang diberikan.
Penyelesaian berkomputer boleh mengangar kesukaran bagi manusia menyelesaikannya, berdasarkan kerumitan teknik menyelesaikan yang diperlukan. Anggaran ini membenarkan penerbit menyesuaikan permainan Sudoku kepada hadiran dengan pengalaman menyelesaikan yang pelbagai. Sesetengah versi di talian menawarkan beberapa tahap kesukaran.
Lihat juga sunting
Rujukan sunting
- Rules and history from the Nikoli website Diarkibkan 2006-06-13 di Wayback Machine
- Keys to Solution at Puzzle Japan
- Let's Make Sudoku! – Explains step-by-step how to make Sudoku puzzles by hand.
- Sudoku Variations article at MAA Online; also includes the history of the puzzle's invention
- Complexity and Completeness of Finding Another Solution and its Application to Puzzles Diarkibkan 2006-07-16 di Wayback Machine Mathematical reference proving NP-completeness.
- Frazer Jarvis's Sudoku page Diarkibkan 2006-02-20 di Wayback Machine Contains programs, data, an article with Bertram Felgenhauer detailing the enumeration of Sudoku grids, and the results of Ed Russell.
- A step-by-step guide to Sudoku by Michael Mepham.
- Commentary on the sudden popularity of Sudoku in Britain:
Pautan luar sunting
- Sudoku di Curlie –Senarai pautan Sudoku aktif
- 'Father of Sudoku' puzzles next move (BBC)
- Platform untuk bersaing di sudoku di peringkat antarabangsa