Sudut jam

Dalam astronomi dan navigasi cakerawala, sudut jam (Jawi: ‏سودوت جم‎code: ms is deprecated ‎) ialah sudut antara dua satah: satu mengandungi paksi Bumi dan zenit (satah meridian), dan satu lagi mengandungi paksi Bumi dan titik penting tertentu (bulatan jam). ^[1]

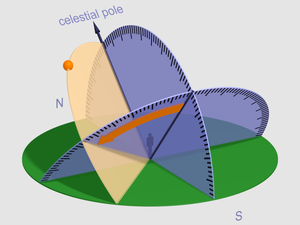
Unitnya mungkin diberikan dalam darjah, masa, atau putaran bergantung pada penggunaan. Sudut boleh dinyatakan sebagai timur negatif satah meridian dan barat positif satah meridian, atau sebagai positif ke arah barat dari 0° hingga 360°. Sudut boleh diukur dalam darjah atau dalam masa, dengan 24 ^jam = 360° tepat. Dalam navigasi cakerawala, konvensyen ini adalah untuk mengukur dalam darjah ke arah barat dari meridian utama (sudut jam Greenwich, GHA), dari meridian tempatan (sudut jam tempatan, LHA) atau dari titik pertama Aries (sudut jam sidereal, SHA).

Sudut jam dipasangkan dengan deklinasi untuk menentukan sepenuhnya lokasi titik pada sfera cakerawala dalam sistem koordinat khatulistiwa . ^[2]

Hubungan dengan jarak hamal sunting

Seperti yang dilihat dari atas kutub utara Bumi, sudut jam tempatan (LHA) bintang untuk pemerhati berhampiran New York (titik merah). Turut digambarkan ialah kenaikan kanan bintang dan sudut jam Greenwich (GHA), masa sisian min tempatan (LMST) dan masa sisiran purata Greenwich (GMST). Simbol ʏ mengenal pasti arah ekuinoks vernal. Dengan mengandaikan dalam contoh ini hari dalam setahun ialah ekuinoks Mac jadi matahari terletak pada arah anak panah kelabu maka bintang ini akan terbit kira-kira tengah malam. Hanya selepas pemerhati mencapai anak panah hijau fajar datang dan menerangi dengan cahaya keterlihatan bintang kira-kira enam jam sebelum ia terbenam di ufuk barat. Kenaikan Kanan bintang adalah kira-kira 18 ^jam

Sudut jam tempatan (LHA) bagi objek di langit pencerap ialah

{\text{LHA}}_{\text{objek}}={\text{LST}}-\alpha _{\text{objek}}

atau

{\text{LHA}}_{\text{objek}}={\text{GST}}+\lambda _{\text{pencerap}}-\alpha _{\text{objek}}

dengan LHA_objek ialah sudut jam tempatan objek, LST ialah masa sidereal tempatan,

\alpha _{\text{objek}}

ialah kenaikan kanan objek, GST ialah masa sidereal Greenwich dan

\lambda _{\text{pencerap}}

ialah longitud pencerap (timur positif dari meridian utama). ^[3] Sudut ini boleh diukur dalam bentuk masa (24 jam ke bulatan) atau dalam darjah (360 darjah ke bulatan)—satu atau yang lain, bukan kedua-duanya.

Sudut jam negatif (−180° < LHA_objek < 0°) menunjukkan objek menghampiri meridian, sudut jam positif (0° < LHA_objek < 180°) menunjukkan objek sedang bergerak menjauhi meridian; sudut jam sifar bermakna objek berada di meridian.

Sudut jam suria sunting

Memerhati Matahari dari Bumi, sudut jam suria ialah ungkapan masa, dinyatakan dalam ukuran sudut, biasanya darjah, dari tengah hari suria. Pada tengah hari suria, sudut jam ialah sifar darjah, dengan masa sebelum tengah hari suria dinyatakan sebagai darjah negatif, dan waktu tempatan selepas tengah hari suria dinyatakan sebagai darjah positif. Contohnya, pada 10:30 pagi waktu ketara tempatan, sudut jamnya ialah −22.5° (15° sejam darab 1.5 jam sebelum tengah hari). ^[4]

Kosinus sudut jam (kos( h )) digunakan untuk mengira sudut zenit suria. Pada tengah hari suria, $h = 0.000$ jadi $kos(h) = 1$ , dan sebelum dan selepas tengah hari suria kos(± h ) = nilai yang sama untuk pagi (sudut jam negatif) atau petang (sudut jam positif), supaya Matahari berada pada ketinggian yang sama di langit pada 11:00 pagi dan 1:00 petang waktu suria. ^[5]

Sudut jam sidereal sunting

Sudut jam sidereal (SHA) bagi jasad pada sfera cakerawala ialah jarak sudutnya di barat ekuinoks vernal yang biasanya diukur dalam darjah. SHA bintang berbeza-beza kurang daripada satu minit lengkok setahun, disebabkan liukan, manakala SHA planet berbeza dengan ketara dari malam ke malam. SHA sering digunakan dalam navigasi cakerawala dan astronomi navigasi, dan nilai diterbitkan dalam almanak astronomi.

Lihat juga sunting

Nota dan rujukan sunting

^ U.S. Naval Observatory Nautical Almanac Office (1992). P. Kenneth Seidelmann (penyunting). Explanatory Supplement to the Astronomical Almanac. Mill Valley, CA: University Science Books. m/s. 729. ISBN 0-935702-68-7.
^ Explanatory Supplement (1992), p. 724.
^ Meeus, Jean (1991). Astronomical Algorithms. Willmann-Bell, Inc., Richmond, VA. m/s. 88. ISBN 0-943396-35-2.
^ Kreider, J. F. (2007). "Solar Energy Applications". Environmentally Conscious Alternative Energy Production. m/s. 13–92. doi:10.1002/9780470209738.ch2. ISBN 9780470209738.
^ Schowengerdt, R. A. (2007). "Optical radiation models". Remote Sensing. m/s. 45–88. doi:10.1016/B978-012369407-2/50005-X. ISBN 9780123694072.

[1] U.S. Naval Observatory Nautical Almanac Office (1992). P. Kenneth Seidelmann (penyunting). Explanatory Supplement to the Astronomical Almanac. Mill Valley, CA: University Science Books. m/s. 729. ISBN 0-935702-68-7.

[2] Explanatory Supplement (1992), p. 724.

[3] Meeus, Jean (1991). Astronomical Algorithms. Willmann-Bell, Inc., Richmond, VA. m/s. 88. ISBN 0-943396-35-2.

[4] Kreider, J. F. (2007). "Solar Energy Applications". Environmentally Conscious Alternative Energy Production. m/s. 13–92. doi:10.1002/9780470209738.ch2. ISBN 9780470209738.

[5] Schowengerdt, R. A. (2007). "Optical radiation models". Remote Sensing. m/s. 45–88. doi:10.1016/B978-012369407-2/50005-X. ISBN 9780123694072.

[1]

[2]

[3]

[4]

[5]